The de Casteljau Algorithm
This is a follow up to Blender and Blossoms.
The de Casteljau Algorithm is a recursive way to calculate the Point on a Bézier curve given its control polygon $$P = \{ \vec{b_i} \}$$ consisting of the Points $$b_i$$. It is defined as follows in the Book:
Given the points $$\vec{b}_0 ... \vec{b}_n$$, $$t \in \mathbb{R}$$ and a function $$f(t): \mathbb{R} \to \mathbb{R}$$. Set
Then $$\vec{b}_0^n$$ is the point with the parameter $$t$$ on the corresponding Beziér curve.
So this is essentially a recursive definition: Starting from $$n$$ points, we always combine two of them and remain with $$n-1$$ points. We continue this scheme until only one point is left. This is the point on the curve for the value $$t$$.
Implementation
The de Casteljau Algorithm is short and beautifully implemented:
import numpy as np
class DeCasteljau:
def __init__(self, *pts, func = lambda t: t):
self._b = np.asarray(pts, dtype=np.float64)
self._func = func
def __call__(self, t):
b, n = self._b, len(self._b)
for r in range(1,n):
for i in range(n-r):
b[i] = (1-self._func(t))*b[i] + self._func(t)*b[i+1]
return b[0]
And this is how it looks.
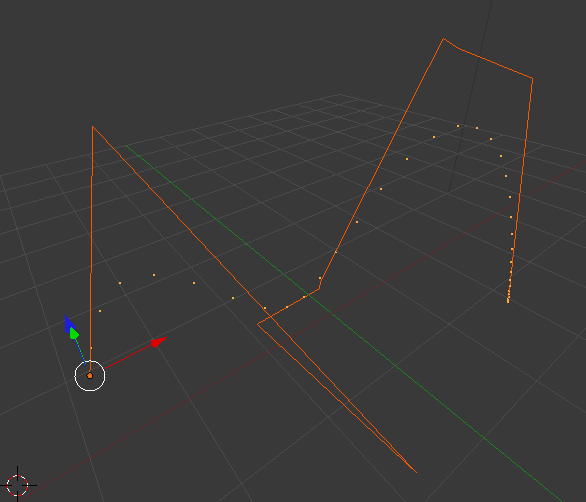
The orange curve is the defining polygon and the dots are the corresponding beziér curve evaluated for 100 values of $$t \in [0,1]$$ and $$f$$ being the identity.
You can find the complete code in the GitHub repository under chap04.
