The AVL Tree
Last post we looked at the Binary Search Tree in some detail and we found
that it is a pretty good data structure. We also found that it behaves like a
linked list and looses its good properties when we insert items in sorted
order. Let's work on this and check out a tree that is auto balancing: the AVL
tree.
The AVL tree is a binary search tree with one new property: in each node, the
height of the left subtree and the height of the right subtree must only
differ by 1 (or zero). That's all there is to it. Let's look at the binary
search tree example we saw the last time and check out what needs to be done
to make it a AVL tree.
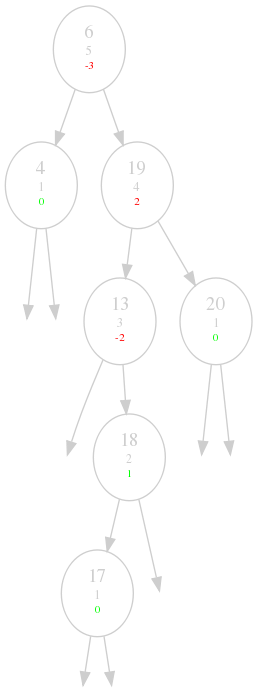
The keys are still written in bigger font size, but I now added two more
properties: the smaller numbers in grey is the height of the node. For a node $$n$$,
with children $$l$$ and $$r$$ the height $$h(n)$$ is simply defined by
\begin{equation*}h(n) = 1 + \mathrm{max}\Big( h(l), h(r) \Big)\end{equation*}The colored number is the height balance of a node, which is just the height of its left
subtree minus the height of its right subtree. So for example the node 13 has no left subtree, so
$$h(l)$$ = 0, the node 18 has height 2, so $$h(r)$$ = 2, this results in a height balance of -2.
The numbers are green when they do not violate the AVL property, otherwise they are red.
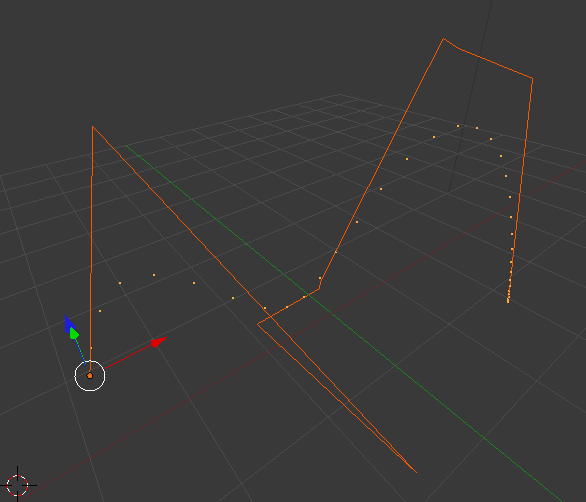
So what do we need to do to fix the 13 for example? Intuitively, we would like
the 13 to go down and the 18 and 17 to come up in some kind of way. But
obviously, we need to keep the ordering of the binary tree. The solution is
quite simple, first, we do a right rotation with the 18 as root, then we do
a left rotate with 13 as the root:
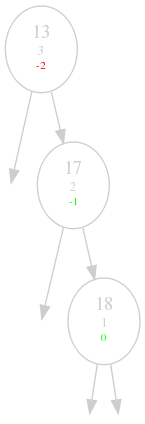
Step 1: 17 moved up and 18 moved down.
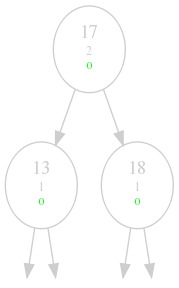
Step 2: 17 moved up and 13 moved down and everything is balanced.
So what is a rotation? For example the left rotation with $$P$$ as root looks like the following. $$R$$ is the right child
of $$P$$.
- $$P$$ becomes the left child of $$R$$
- $$R$$'s left child becomes $$P$$'s right child
That basically means that $$P$$ comes down while $$R$$ goes up. The
right rotation looks the same, but right and left swapped.
What changes for the handling of the tree? Searching and traversing stays the
same, it is a binary search tree after all. What about insertion and deletion?
Insertion
Insertion is simple: we just insert the node where it belongs, but than we
have to make sure that the AVL property is not violated anywhere. It isn't
automatically violated after insertion, but if it is, it can only be violated
in one node which is on the path we took while going down the tree. We
rebalance this node and are done.
def _just_inserted(self, node):
"Node was just inserted into the tree"
par = node.parent
while par:
self._update_height(par) # Recalculate the height of the parent
if abs(par.height_balance) > 1:
self._rebalance(par) # Rebalance the one node and stop
break
par = par.parent # Otherwise continue with parent
return node
Deletion
Deletion is also easy: The case of a node with two children doesn't change and
the deletion in the other cases are just the same. But the height of all the
nodes on the path we took down to the nodes might have changed, so we have to
check for this and rebalance accordingly. If we encounter a node on our way up
that has not changed height, we can stop checking because the nodes above
it will not feel any difference.
def _delete_leaf(self, n):
par = n.parent
BinarySearchTree._delete_leaf(self, n)
self._rebalance_till_root(par)
def _delete_node_with_one_child(self, n):
par = n.parent
BinarySearchTree._delete_node_with_one_child(self, n)
self._rebalance_till_root(par)
def _rebalance_till_root(self, node):
while node and self._update_height(node):
node = node.parent if \
abs(node.height_balance) <= 1 else self._rebalance(node)
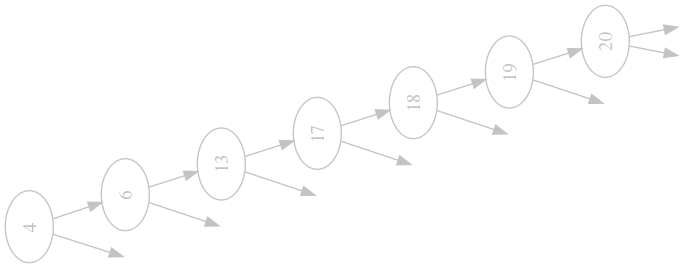
That's all there is to it. Let's repeat our ending experiment from the last
time and insert our values in sorted order in our shiny new data structure:
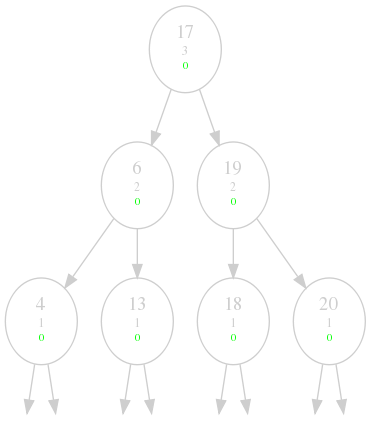
Perfect. But how good is it in the general case?
Number of nodes in the tree
Given $$m$$ nodes, what will be the height of the tree be like? Well, it
will likely be some kind of logarithm $$m$$. Let's check this more
closely.
Let's define $$n(h)$$ to be minimal number of nodes in a tree of
height $$h$$. There is an easy formula for that: the smallest number of
nodes is when the left subtree has an height of h-1 and the right h-2, so
\begin{equation*}n(h) = n(h-2) + n(h-1) + 1\end{equation*}I will state that the following is true and proof it by
induction later on.
\begin{equation*}n(h) \geq c^{h-1}\end{equation*}The question is, what will the biggest $$c$$ be that still solves
this inequality? Let's solve for c:
\begin{eqnarray*}(h-1) \log c & \leq & \log n(h) \\
c & \leq & \exp \Big\{ \frac{\log n(h)}{h-1} \Big\}\end{eqnarray*}Here are some numbers:
| h |
$$n(h)$$ |
max $$c$$ |
| 3 |
4 |
2 |
| 4 |
7 |
1.9129 |
| 7 |
33 |
1.7910 |
| 20 |
17710 |
1.6734 |
| 50 |
32951280098 |
1.6392698637801975 |
Let's do the induction finally. We assume that the condition holds for smaller values, we than only have
to show that it also holds for $$n$$:
\begin{eqnarray*}n(h) & = & n(h-2) + n(h-1) + 1 \\
& \geq & c^{h-3} + c^{h-2}\end{eqnarray*}\begin{equation*}c^{h-1} \leq c^{h-3} + c^{h-2}
\Rightarrow c^2 - c - c \leq 0\end{equation*}The only positive solution of this quadratic equation is the golden ration:
\begin{equation*}c_{\max} = \frac{1 + \sqrt{5}}{2} \approx 1.618\end{equation*}Let's assume we have a tree with height $$h$$ and $$m$$ nodes in it. Now we know:
\begin{eqnarray*}m \geq n(h) &\geq & c_{\max}^{h - 1} \\
\Rightarrow \log_{c_\mathrm{max}} n(h) + 1 & \geq & h\end{eqnarray*}And because the $$\log$$ function is monotonous:
\begin{equation*}h \leq \log_{c_\mathrm{max}} m + 1\end{equation*}Pretty well balanced it is, indeed.
Conclusion
We continued our investigation of binary search trees and looked at a self
balancing version of it, the AVL tree. We discussed the basic principle of how
it works without going into all the individual cases one would encounter when
deleting or inserting (you can find them elsewhere). We also looked at code
that implement the differences compared to the normal binary search tree.
More information is of course on Wikipedia. The proof of height was stolen
from the computer science lectures by Dr. Naveen Garg about AVL trees, he
does a great job of making things clearer.
Remember, there is source code for this post on github. I added an
implementation of an AVL tree that derives from an ordinary binary search tree
and only implements the additional stuff we talked about.
Next time, we will look at Red-Black Trees.