The binary search tree
Let's suppose you want to keep some data in memory. Occasionally, new items arrive, old items get unimportant and you want to delete them. Adding new items and deleting old should not take long. And you want to be able to traverse the data quickly and in sorted order at all points in time.
Arrays are out, because they would shuffle all the elements around on deletion and insertion. What data structures would you use?
Why not use a binary search tree? It only needs $$\mathrm{O}(n)$$ space and insertion and deletion take on average only $$\mathrm{O}(\log n)$$ time. A pretty good deal?
What is it?
This is one for integers. You can put everything that can be ordered inside a binary search tree, but for simplicity, we will stick with integers.
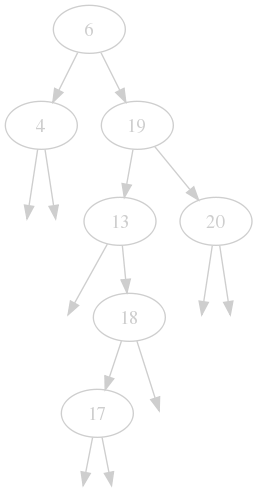
Our tree has 7 nodes in it, so $$n = 7$$. The root node is 6. See the nodes 19 and 6? They have 2 children: left and right. All nodes also have a parent. There are other nodes with either a left or a right child. There are also some nodes without any children, they are called leafs of the tree.
This is called a binary tree because every node can only have a maximum of two children. But what makes it a binary search tree? If you look closely, you will realize that all children that are to the left of a node are strictly smaller and the reverse for the right site. Look at the 19: 20 is to its right and bigger, 6, 4, 13, 18, 17 are to its left and strictly smaller. And that's all there is to it.
Searching & Insertion
This property makes it easy to check if a value is inside our tree. For example, if you want to know if 12 is in the tree you do the following:
- Start at the root: 12 > 6 so go right,
- 12 < 19 so go left
- 12 < 13 so go left again... Ups.
There is no node here. Well, 12 is not in our tree, is it? But if you would want to insert it, you would do it right here, as left child of 13.
Let's look at the python code for those two operations:
def search(node, key):
if node is None: return None
if node.key == key: return node
return search(node.l, key) if key < node.key else \
search(node.r, key)
search(root_node, 12) # None, for our case
def insert(node, key):
if node is None: return Node(key)
if key <= node.key:
node.l = insert(node.l, key)
node.l.parent = node
else:
node.r = insert(node.r, key)
node.r.parent = node
return node
insert(root_node, 12)
Note that we also do some house holding that the links between children and parents are valid after insertion.
Deleting
Deleting an item is a bit hairy, but there are only three cases:
- Delete a leaf: Just remove it and you're done. Remember to break the links to its parent though!
def delete_leaf(n):
if n.parent.l == n:
n.parent.l = None
else:
n.parent.r = None
- Delete a node with one child: we essentially remove this node from the chain by linking its parent to its child.
def delete_node_with_one_child(n):
child = n.l or n.r
if n.parent.l == n:
n.parent.l = child
if n.parent.r == n:
n.parent.r = child
child.parent = n.parent
Delete a node with two children. This is the most difficult one. Look at 19, how could you remove this from the tree? Well, we have to keep the ordering property. So the only two values that we could use in this position that would keep the property are 18 and 20. Those are the biggest item in its left subtree (18) and the smallest item in its right subtree (20). And this is always the case! Which one should we pick? It doesn't matter, but picking one at random will help distribute the items in our tree evenly.
Now all that is left to do is to delete the node we took the value from.
import random
def biggest_successor(node):
if node.r:
return biggest_successor(node.r)
return node
def smallest_successor(node):
if node.l:
return smallest_successor(node.l)
return node
def delete_node_with_two_childs(n):
child = smallest_successor(n.r) if random.choice((0,1)) == 0 \
else biggest_successor(n.l)
n.key = child.key
delete_node(child) # could have one or zero children
Traversing the Tree
Now how about getting at the elements in sorted order? We would need to start at the leftmost element in the tree because it is the smallest. The next bigger one is the smallest element in its right subtree. We can express this in a recursion quite nicely:
def iter_tree(node):
if node.l:
for k in iter_tree(node.l):
yield k
yield node
if node.r:
for k in iter_tree(node.r):
yield k
list(root_node) # -> [4, 6, 13, 17, 18, 19, 20]
Is it a deal?
So we have a nice data structure now, should we use it? Yep. Can we achieve better? Not in the average case. Is is good for all cases? Well, just imagine your data arrives already in sorted order:
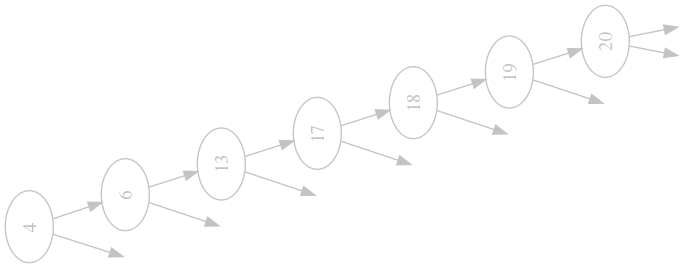
Terrible! Gone is our $$\mathrm{O}(\log n)$$ search time (it is $$\mathrm{O}(n)$$ now). And with it the nice performance of inserts and deletions. What can we do about it? There are some more advanced trees that are able to keep themselves balanced, that means that there are around the same number of nodes in each subtree of each node. We will look at AVL Trees and Red-Black Trees in future installments of this series.
Conclusion
We took a quick glance at binary search trees, how they work and why they are useful. We discussed how easy insert is and that deletion is quite straightforward, but there are many different cases. We also looked at python snippets that implemented the functionality we talked about.
If you want to know more you can either hop over to Wikipedia and read it up for yourself. Or, you can watch the excellent computer science lectures by Dr. Naveen Garg about data structures - especially trees.
Or you could check out the source code for this post on github. There you will find my implementation of a binary search tree and also the visualization routine I used to make the images of our tree here.